An Explanation for Why Proteins Crystallize in Certain Strongly Preferred Space Groups
One of the most striking observations in crystallography is that molecules seem to prefer to crystallize in a relatively small number of preferred space group symmetries. For (chiral) macromolecules there are 65 possible space group symmetries. Out of these 65 possibilities, the single most frequently obtained space group (P212121) accounts for about 30% of all macromolecular crystals. At the other end of the spectrum, the space groups representing the lower half, taken together, account for less than 1% of all observed crystals. This phenomenon can be viewed as a test of our understanding of crystallization, and the solid state in general.The unequal occurrence of the space groups was analyzed first in the context of crystals of small organic molecules. In particular, the Russian crystallographer Kitaigorodsy along with Scottsman Jack Dunitz and American Carolyn Brock contributed to the analysis in organic molecules. A general, but non-mathematical, understanding was held that the preferred space groups were those that allowed for the tightest packing of molecules; crystals of organic molecules tend to be very tightly packed. The problem with extending that idea to macromolecules was two-fold. First, protein crystals are not at all tightly packed; they are composed of nearly 50% solvent on average. Furthermore, protein crystals in the most favored space groups are not packed much more tightly than protein crystals in less-favored space groups. Consequently, it was hard to see how packing density could account for the observed preferences, which range over more than two orders of magnitude between the most and least favored space groups. Secondly, small organic molecules and large macromolecules do not prefer the same space groups; there are some similarities but the differences are clearly significant. The situation for macromolecules therefore required a different explanation.
In 1995, a mathematical explanation was provided by a graduate student, Stephanie Wukovitz (Wukovitz and Yeates. 1995. Why protein crystals favour some space-groups over others. Nat. Struct. Biol. 2, 1062-7). Instead of considering packing, her analysis considered connectivity between molecules in the crystal, established through non-covalent contacts between protein molecules. The reasoning was that in order for an assembly of molecules to constitute a solid three-dimensional crystal, the molecules all had to be part of a connected network. Otherwise, one would have disconnected layers for instance. The connection to space group preference was that the requirements for connectivity might impose different numbers of restrictions on arrangements built under different symmetries. We showed that for a given space group symmetry, there was a minimum number of unique contacts, which we called C, that was always required. This quantity is a mathematical property of the symmetry group, and not a property of the molecules in question. This fundamental property of the space groups had not been discussed before. The minimum contact number, C, is illustrated at the right for two different plane groups. Obtaining the value of C for the 65 space groups was extremely difficult. We were unable to find an analytical solution -- Stephanie contacted famed mathematician Coxeter, who told her he knew of no closed solution -- so a numerical solution was obtained computationally.
The new quantity C elucidated by Wukovitz was combined with other standard quantities relating to the space groups (e.g. number of independent unit cell parameters), to obtain the critical dimensionality parameter, D, which is the total number of rigid body degrees of freedom available to a collection of molecules under the requirement that they obey a chosen space group symmetry, and that they are connected to each other by contacts. Another way of imagining the meaning of D is to think about n protein molecules. Taken together they have 6n-6 internal rigid body degrees of freedom (subtracting 6 removes the irrelevant motion of the molecules as an intact group). Therefore, every possible configuration of the molecules can be described as a point in 6n-6 dimensional space. Only a tiny fraction of that space corresponds to configurations that would constitute a crystalline arrangement. All the configurations that would constitute a crystal in a particular space group symmetry fall in some subspace. What is the dimensionality of that subspace for each space group symmetry? The value is the quantity D. Obtaining the value of D requires taking into account all the restrictions that the molecules must obey. Critical in the analysis is the restrictions that arise from the requirement for connectivity between the molecules; the value of D could only be calculated given knowledge of C.
Wukovitz found that the value of the dimensionality, D, calculated from purely mathematical reasoning, ranged from 4 to 7 for the 65 space group symmetries; the analysis thereby divided the 65 space groups into 4 categories (D=4, 5, 6, or 7), without any reliance on observed data. The correlation between the categories and the observed frequencies with which the space groups are observed was striking at the time, and has become even more striking with updated analyses based on a much larger database of protein crystals than was available in 1995 (see Chruszcz, et al. 2008. Protein Science, 17, 623-632). The protein crystallographer's favorite space group, P212121, is the only one for which D=7. After this top space group, the twelve next most commonly observed space groups are all in the category D=6. In fact they account for 12 of the 13 space groups in that category; one space group I212121 has D=6 but is rarely observed for reasons explained by Wukovitz -- the minimum contact number cannot be realized with molecules having compact shapes.
Besides providing a striking explanation for the observed preferences, the theory gave rise to one unusual prediction having to do with what would be expected if one could synthesize macromolecules in both 'hands' or enantiomers and then crystallize them. So-called racemic mixtures of chiral molecules can crystallize in 230 different space groups; 155 additional cases beyond the 65 possible for purely chiral samples are possible. The theory predicted that one particular space group, P1(bar), would be preferred. This was particularly significant because the preferred space group for racemic mixtures of organic molecules is a different space group, P2/c. At the time Wukovitz' NSB paper was published, a single case study was available. Jeremy Berg's group had crystallized a racemic mixture of rubredoxin after synthesizing the left-handed version from all D-amino acids (Zawadzke and Berg. 1993. Proteins 16, 301-5). Berg's crystal was indeed in space group P1(bar).
In the years afterwards, a few crystals of small, chemically synthesized proteins or oligonucleic acids were grown from racemic mixtures, and those few were indeed in space group P1(bar) (or pseudo P1(bar)) (see Hung and Kim, et al. 1999. JMB 285, 311-321; Patterson and Eisenberg, et al. 1999. Prot. Sci., 8, 1410-1422). Interest in synthesizing and crystallizing racemic protein mixtures on a larger scale has been revived recently by Stephen Kent (see Pentelute, et al. 2008. J. Am. Chem. Soc., 130, 9695-9701), whose earlier invention of 'native chemical ligation' methods for chemically synthesizing larger proteins made this tractible. Kent's recent results also support the prediction of P1(bar) as the most probable space group for racemic macromolecular crystals. These studies bear out the specific prediction made in the 1995 Wukovitz paper, and therefore add confidence to the ideas put forward there for why proteins crystallize in certain preferred symmetries. The remarkable agreement between recent results and these earlier predictions is highlighted in a Commentary by Brian Matthews and references therein (Matthews, 2009. Protein Sci. 18, 1135-8).
Despite the success of Wukovitz and Yeates (1995) in understanding space group preferences in macromolecules, that analysis provides an incomplete picture. For example, in the category of space groups with D=6, there is a considerable spread in terms of observed frequencies. These differences must relate to other properties, probably more molecular than mathematical in nature. Further analysis is required to achieve a fully predictive understanding (see Chruszcz, et al. 2008. Protein Science, 17, 623-632).
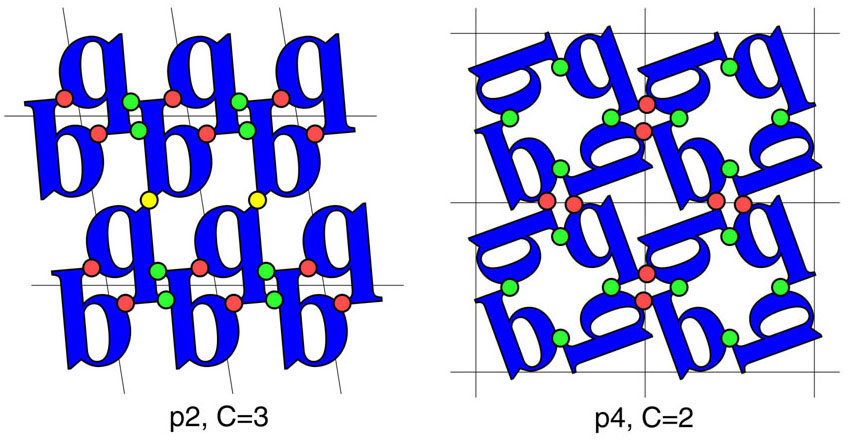
Illustration of the minimum contact number, C, for two different plane groups, p2 and p4. Molecular connectivity in p2 requires a minimum of three distinct contact types, whereas at least two are required for p4. The minimum contact number derives from the properties of the symmetry group and has virtually nothing to do with the molecule in question. The value of C figures prominently in how many rigid body degrees of freedom (D) are available to a set of molecules that is to assemble into a given space group symmetry; the degrees of freedom available appears to be largely responsible for the space group frequency phenomenon, at least for macromolecules. See Wukovitz and Yeates. 1995. Why Protein Crystals Favour Some Space Groups Over Others. Nature Structural Biology 2, 1062-1067.