|
The Maximum Contact Radius --
Algorithms for analyzing protein surfaces and their accessibility to
solvent (i.e. water molecules) were first developed in 1971
(Lee and Richards, JMB 55, 379-400).
Solvent accessibility calculations provide a detailed, or short-range
description of protein surfaces, and are well suited for analyzing
physiochemical properties relating to interactions between proteins
and water. However, they do not provide a very rich description
of longer-scale properties of a protein surface,
which are relevant for accessibility to binding larger molecules,
such as other proteins, antibodies, receptors, etc. In order to
address such issues, other measures of protein surface accessibility arose.
In 1986 Novotny examined the utility of calculating the largest
probe radius that could contact a given atom in a protein (Novotny, et al. 1986.
PNAS 83, 226-230), and similar ideas were explored by Tainer and Getzoff (Geysen, et
al. 1987. Science 235, 1184-1190). The approaches used for calculating
the sphere of largest contact were numerical,
following methods introduced by Kuntz for filling binding sites with spheres
(Kuntz, et al. 1982. JMB 161, 269-288). Briefly, a sphere surrounding
each atom in question
was covered with dots, and then the largest sphere that could
be drawn tangent to that point without colliding with any other atoms
was determined. The point
on the surface of the atom with the largest radius of accessibility was then
identified. This method provided a practical solution
to the problem, but left open the question of how one might obtain an
analytical solution that was computationally tractable. The problem was
that a naive approach to an analytical solution grew as O(n5), where
n is the number of atoms in the structure. [The largest sphere that touches
an atom will in general touch three other atoms, but cannot contain any other
atoms in its interior; therefore four atoms define a sphere and the remaining
atoms have to be checked to see if any fall inside the defined sphere].
A rapid analytical solution to the problem was described in 1995
(Yeates. 1995. Algorithms for Evaluating the Long-Range
Accessibility of Protein Surfaces. JMB 249, 804-815).
The numerical approaches that were already available
were fast and provided reasonably accurate values for the maximum contact
radius, so the analytical approach did not fill an important
void. Nonetheless, the method of solution was interesting and highly
unusual. The solution relied on an obscure trick (not
illustrated here) -- but one that
was familiar to the artist M. C. Escher -- that involves inversion in a
circle (or a sphere in the 3-D case here). This trick, which also
shows up in mathematics in the category of conformal mapping, takes
everything inside a sphere and maps it outside, and vice-versa. A property
of the transformation is that lines (or planes) are mapped onto circles (or
spheres), and vice-versa. Application of this trick to the
problem of identifying the largest contact sphere succeeded in mapping the problem
of finding a sphere to a problem of finding a plane. This linearization allowed
simpler approaches (e.g. finding the convex hull) to be used to solve a much
harder problem involving spheres.
Diffusion Accessibility -- In the same paper (Yeates. 1995. Algorithms for Evaluating the Long-Range Accessibility of Protein Surfaces. JMB 249, 804-815), an entirely new description of long-range accessibility was introduced (see figure) and called diffusion accessibility. In this description, the degree to which a point or atom on a protein surface is said to be accessible is determined by the fraction of the time that a diffusing probe molecule would collide with this point on the protein surface, before being captured by collision with some other point on the protein surface. This parameter gives a long-range description of surface geometry. For instance, an atom that is highly exposed to solvent (i.e. based on a traditional solvent accessibility calculation), but which resides at the bottom of a pronounced depression in the protein surface, would end up having a low diffusion accessibility; a randomly diffusing probe molecule would most likely collide with another part of the protein surface before reaching the point on the depressed surface. Calculating the diffusion accessibility is simple in theory. One could simply conduct a very large number of random walks and keep track of the captures (figure, top panel). But this is computationally intractable if one wishes to do enough simulations to obtain accurate capture rates for individual parts of the surface. Fortunately, the problem can be solved in a more powerful fashion by recognizing that it can be treated as a problem in steady state diffusion, with a sphere surrounding the protein acting as a source, and the protein surface acting as a sink (figure, lower panel). The diffusion equation at speady state can then be solved on a grid, using the same kinds of methods used to do Poisson-Boltzmann electrostatics calculations. Specifically, at steady state the Del-squared of the concentration of the hypothetical diffusing probe must be zero everywhere between the source and the sink. Solving the large system of linear equations leads to a value for the concentration across the grid, from which the flux across the protein surface at any point can be calculated easily. Because protruding regions of a protein would be expected to capture a diffusing probe by first-collision more frequently than regions of a protein surface that lie in depressions, diffusion accessibility can give a useful picture of surface depth and concavity. In order to make the calculation of diffusion accessibility easily accessible for the purposes of improving visualization of protein and nucleic acid structures, a web-server is available to do the necessary calculation and to provide scripts for coloring using the program PyMol. The web server for diffusion accessibility is here. |
Diffusion Accessibility figures from
JMB 249, 804-815, 1993.
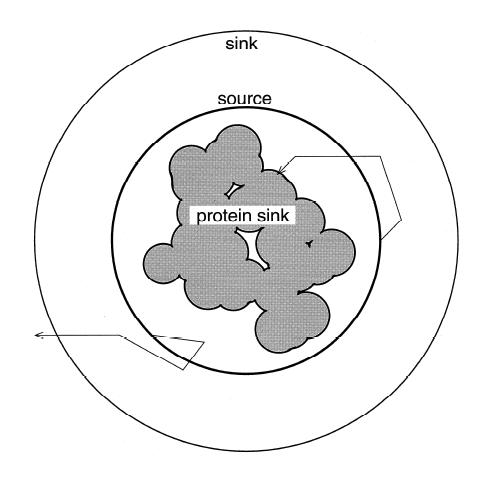 Diagram describing calculation of diffussion accessibility by random walk simulations. 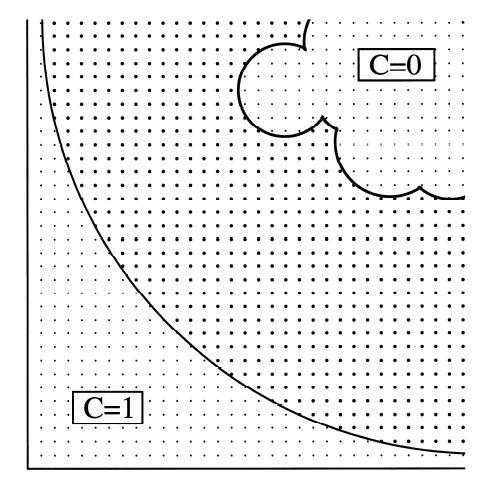 Diagram describing calculation of diffusion accessibility by numerical solution of the equations of diffusion at steady state on a grid. |