|
A first foray into twinning - Doug Rees
had worked on a twinned protein crystal as a student with
Lipscomb, and had brought an interest in methods for dealing with
twinned crystals when he arrived at UCLA. One of my first projects
as a student with Doug was to figure out if there was a way to disentangle isomorphous replacement
data in the presence of twinning, particularly if the twinning fraction
was high enough to prevent 'detwinning' (i.e. recovering the true crystallographic
intensities from the twinned observables). The underlying problem was
that the typical equations upon which MIR is based -- which relate the
complex quantities FP, FPH, fh -- were
of no use if the values of the
individual quantities were unknown. My first publication was a solution
to this problem of phasing in the presence of (even perfect) twinning.
The solution involved casting the ordinary phasing problem (e.g. phase circles)
into four dimensions; phase circles became hyperspheres in 4-D. This
was necessary to account for the mixing of the real and imaginary components
of two different twin-related reflection. For example, an observed intensity
gave the value for the sum of two separate crystallographic intensities,
meaning that Iobs =
A12 +
B12 +
A22 +
B22
(where A1 is the real part
of the structure factor for the first twin-related reflection, and so on);
this is an equation for
a hypersphere. Information from the heavy atom phasing model then gave
additional hyperspheres, whose intersections eventually made it possible
to extract out the correct real and imaginary parts of the two separate
structure factors, despite the absence of direct measurement of the individual
reflection intensities. An Acta A paper published in 1987
(Acta Cryst. A43, 30) provided the necessary
theory and a synthetic test case. In the meantime, solving twinned crystal structures
by molecular replacement turned out to be relatively routine -- as a
student, Matt Redinbo
published the first molecular replacement structure from a perfectly twinned protein crystal
(Acta Cryst. D49, 375 (1993)). In constrast, no highly
twinned structures have been phased by MIR methods using the general solution
described in the 1987 Acta paper. Experimental phasing (MIR or anomalous) has
been successful in
cases of lower twin fraction by correcting ('detwinning') the observed data,
or in some cases of high twin fraction by essentially ignoring the
twinning during the phasing stages and incorporating it only later in
the refinement stage.
Twin fraction estimation - Numerous methods had been described for estimation the twin fraction, but a particularly simple one emerged from an analysis that involved taking a pair of reflection intensities and reducing them to an effectively normalized or unitless quantity by dividing their difference by their sum, giving a value between -1 and 1, or between 0 and 1 if the absolute value is taken. This parameter was called H. When the two observed reflections in question are related to each other by twinning (meaning both are derived from partial mixing of two separate twin-related reflection intensities), the statistical distribution for the parameter H is uniform, and has a simple dependence on the twin fraction, alpha. This led to a particularly simple way of examining diffraction data and estimating the twin fraction (Acta Cryst A44, 142 (1988)). Local statistics for detecting twinning - As noted above, good methods were available for estimating the twin fraction in crystals suffering from partial twinning by evaluating the overall degree of similarity between pairs of twin-related reflections. In addition, numerous stastical analyses had been developed for detecting cases in which perfect twinning was involved. In perfect twinning, the twin-fraction is 1/2, causing erroneously high symmetry to appear in the diffraction pattern. This situation presents a different kind of challenge compared to partial twinning. In a case of perfect twinning, the problem is not to determine the twin fraction, but rather the problem is to recognize that the observed diffraction data suffer from high or perfect twinning by examining the overall intensity statistics, which deviate significantly from theoretical Wilson statistics. The complication is that sometimes other kinds of crystallographic issues interfere with the intensity statistics, and can defeat the traditional tests for twinning that simply look at the cumulative distribution of normalized intensities. One confounding problem is anisotropy, which tends to give more extreme distributions of intensities. To overcome this problem, a new equation was introduced that examines the differences between pairs of reflections near each other in reciprocal space; an equation similar to the one used for comparing twin-related intensities in the partial twinning test was adopted, but here the reflection pairs are nearby rather than twin-related. The statistics for this parameter (called L) relating local pairs of reflections were found to be simple for both the situation of normal (untwinned) data and perfectly twinned data. The use of the measure L therefore provides a test for perfect (or high) twinning that is robust to anisotropy (Padilla and Yeates, Acta D59, 1124-1130 (2003)). In addition, pseudo-centering in a crystal can lead to confounding effects similar to anisotropy, and the local test can overcome this situation as well if the reflections to be compared are chosen properly. |
 A highly schematic diagram of hemihedral twinning. Two crystal domains are shown that obey P4 symmetry. The 180 degree twin operation that relates the two domains superimposes their reciprocal lattices. 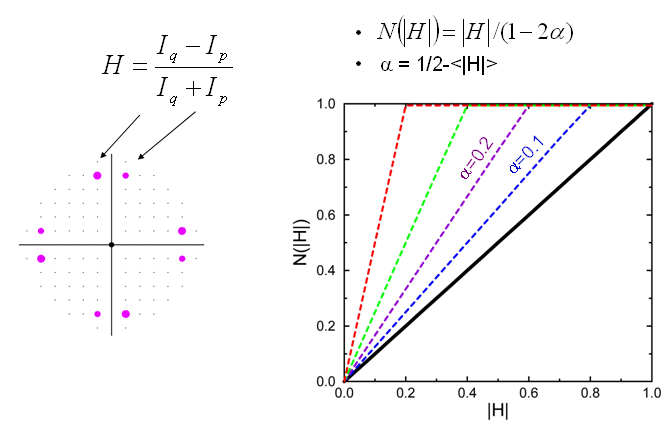 Definition of a parameter, H, that relates the observed
values of two twin-related intensities. The statistics
of H have a simple form as a function of the twin
fraction, alpha, thereby providing a simple approach
for estimating the twin fraction in cases of partial
twinning (Yeates, T.O. Acta Cryst A44, 142 (1988)).
Definition of a parameter, H, that relates the observed
values of two twin-related intensities. The statistics
of H have a simple form as a function of the twin
fraction, alpha, thereby providing a simple approach
for estimating the twin fraction in cases of partial
twinning (Yeates, T.O. Acta Cryst A44, 142 (1988)).
 Definition of a parameter, L, similar in form to H, but
relating two reflections nearby (or local) in reciprocal space.
The behavior of L is sensitive to the presence of twinning,
and is not affected adversely by anisotropy in a data set,
and so is particularly effective in testing for perfectly
twinned or highly twinned data (Padilla and Yeates, Acta
Cryst. D59, 1124-1130 (2003)).
Definition of a parameter, L, similar in form to H, but
relating two reflections nearby (or local) in reciprocal space.
The behavior of L is sensitive to the presence of twinning,
and is not affected adversely by anisotropy in a data set,
and so is particularly effective in testing for perfectly
twinned or highly twinned data (Padilla and Yeates, Acta
Cryst. D59, 1124-1130 (2003)).
|