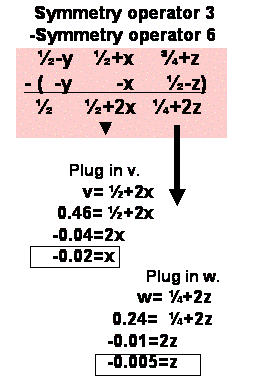| Objective: To determine the mercury position
(x,y,z) from a difference Patterson map calculated with data from the PCMBS
derivative crystal.
Method:
1) Label each difference Patterson peak with its
(u,v,w) coordinates read from the difference Patterson map. The coordinates
of each peak corresponds to a vector difference between one pair of crystallographically
related heavy atoms (i.e. atoms related by space group symmetry operators).
The mathematical expression for the difference vector is given by taking
the difference between each pair of symmetry operators in the space group.
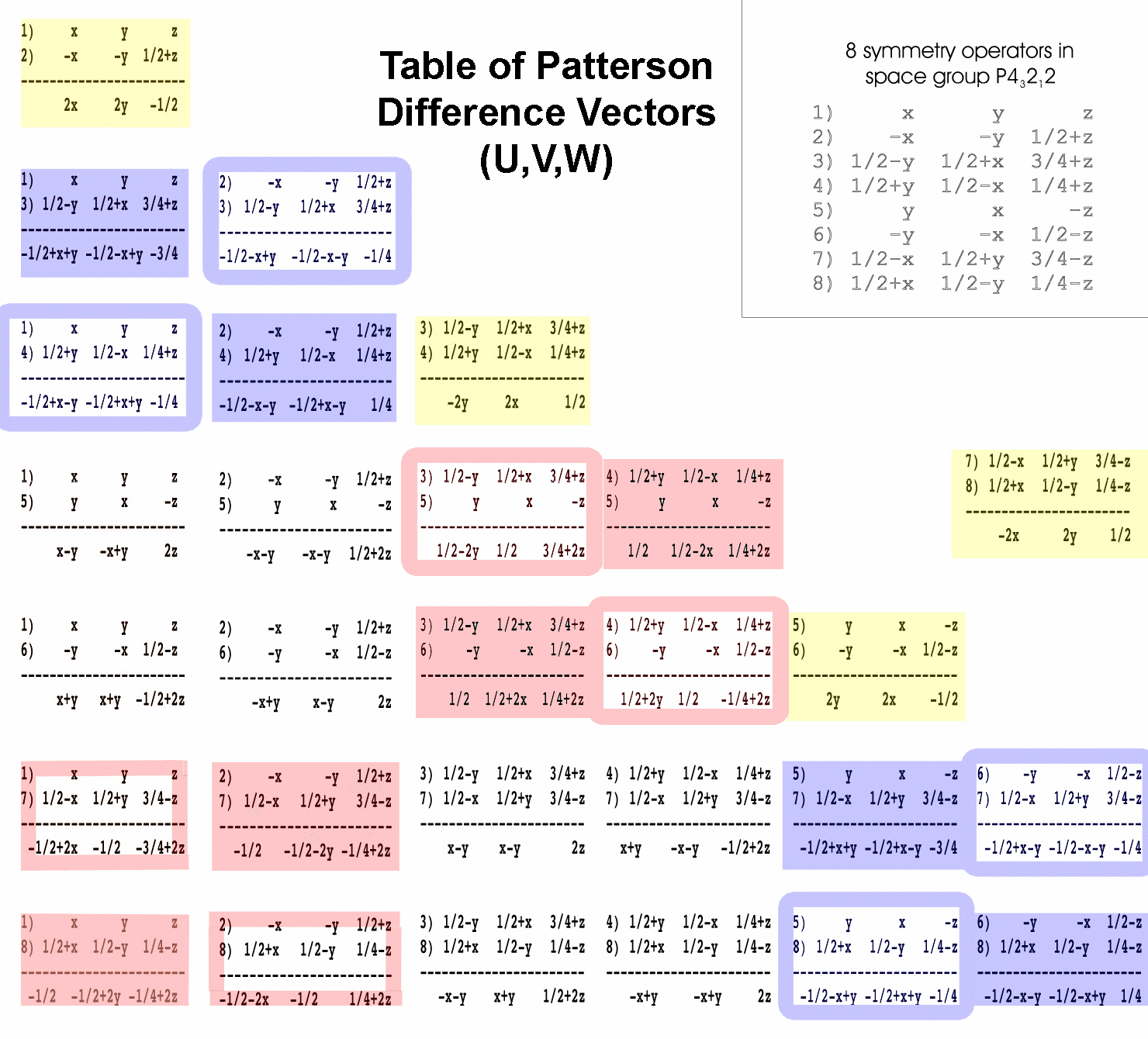
2) Assign each of the labeled peaks with the difference
vector equation that describes it. There are 8 symmetry operators in
space group P43212 so there are 82-8=56
possible difference vectors to choose from in your assignment. Difference
vectors between each pair of symmetry operators from the P43212
space group have been calculated for you (see table of Patterson difference
vectors below). OK, actually, 28 difference vectors are calculated
below; the remaining 28 are just the same except the signs are negated in
the result (i.e. symop#3-symop#1 is the negative of symop#1-symop#3).
To help you choose the appropriate difference vector for each peak, the difference
vectors have been color coded. Difference vectors in the blue boxes produce
peaks on the w=1/4 or w=3/4 section. Difference vectors in the yellow
boxes produce peaks on the w=1/2 section. Difference vectors in the red boxes
produce peaks on the u=1/2 or v=1/2 sections. These sections are called
Harker sections. Let's begin with a peak on the w=1/4 Harker section. This
peak must have been produced by one of the pairs of symmetry operators shown
in blue boxes. Does it matter which of the blue boxed equations I use?
Well, yes and no. Yes, it makes a difference in the numerical
value obtained in the result. But, these values should all be equivalent
by crystallographic symmetry. Remember, if there is a single heavy atom in
the asymmetric unit, then there will be seven other symmetry equivalents
in the unit cell, these are related by the crystallographic symmetry operators.
By chosing a different blue boxed equation, you will be solving for a different
symmetry equivalent. It's OK. Just pick one. Write the equation
in the margin, next to the peak. (Technical note: actually there are
more than just eight possible correct (x,y,z) answers you could obtain. There
are 8*4=32 possible different correct answers. The 24 additional
possible correct answers arise from the arbitrary choice of origin. If
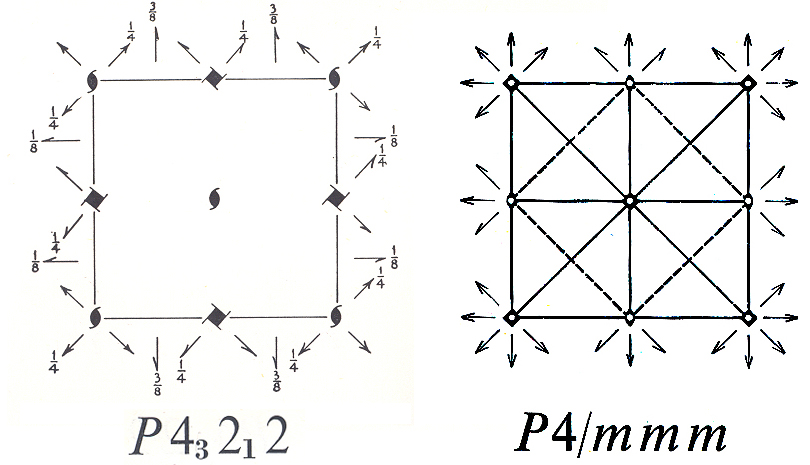
you look at the symmetry diagram for space group P43212
shown above, you will see that by adding (1/2,1/2,0), or (0,0,1/2), or (1/2,1/2,/1,2)
to x,y,z the atom would remain in the same symmetry environment. The
particular origin that is chosen will affect the numerical value of x, y,
or z, but they do not its validity. The 32 symmetry operators that relate
these alternative correct choices are called Cheshire symmetry operators
and are given below.
3) Solve for the x,y coordinate of the heavy atom.
Plug u and v (coordinates of the Patterson peak) into the equation and solve
for x and y (coordinates of the heavy atom). OK, that was easy; I have x
and y. But, I still need z!
4) Solve for the z coordinate of the heavy atom.
Chose a peak on the u=1/2 section. Find the corresponding difference vector
equation. Plug in the v,w coordinates to Solve for x and z.
5) Check for consistency in the x coordinates derived
from the steps 3 and 4. We would like to combine the x,y coordinates
from step 3 with the z coordinate derived from step 4 in order to get a complete
set of x,y,z coordinates for the heavy atom. But, before we do this, we must
check that the x coordinate derived from both sections agree. If they
agree, then we have our x,y,z. But, if the two values of x do not agree
then you must find a symmetry operator that transforms x from step 3 to have
the same value as the x from step 4, and then use this symmetry operator
to transform y from step 3 so it is consistent with x and y from step 4.
After all this we should have a self consistent set of x,y,z. What symmetry
operator do I use? It can be any of the Cheshire symmetry operators
for this space group.
Cheshire Symmetry Operators
for space group P43212
X, Y, Z
-X, -Y, Z
-Y, X, 1/4+Z
Y, -X, 1/4+Z
Y, X, -Z
-Y, -X, -Z
X, -Y, 1/4-Z
-X, Y, 1/4-Z
1/2+X, 1/2+Y, Z
1/2-X, 1/2-Y, Z
1/2-Y, 1/2+X, 1/4+Z
1/2+Y, 1/2-X, 1/4+Z
1/2+Y, 1/2+X, -Z
1/2-Y, 1/2-X, -Z
1/2+X, 1/2-Y, 1/4-Z
1/2-X, 1/2+Y, 1/4-Z
X, Y, 1/2+Z
-X, -Y, 1/2+Z
-Y, X, 3/4+Z
Y, -X, 3/4+Z
Y, X, 1/2-Z
-Y, -X, 1/2-Z
X, -Y, 3/4-Z
-X, Y, 3/4-Z
1/2+X, 1/2+Y, 1/2+Z
1/2-X, 1/2-Y, 1/2+Z
1/2-Y, 1/2+X, 3/4+Z
1/2+Y, 1/2-X, 3/4+Z
1/2+Y, 1/2+X, 1/2-Z
1/2-Y, 1/2-X, 1/2-Z
1/2+X, 1/2-Y, 3/4-Z
1/2-X, 1/2+Y, 3/4-Z
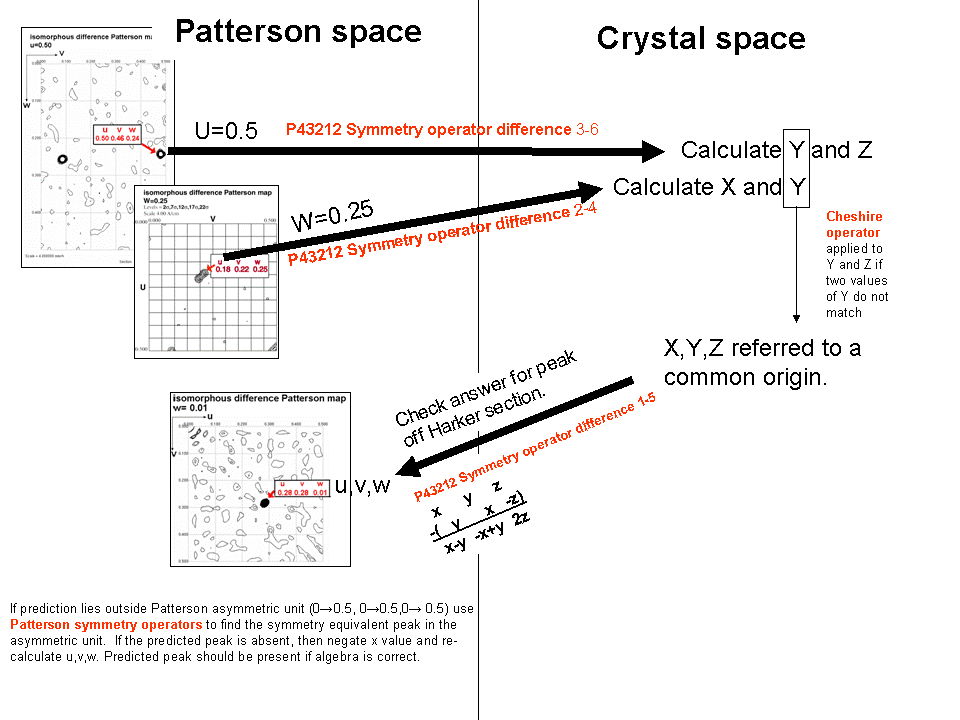
6) Check that xyz can predict the position of a third
Patterson peak, not lying on a Harker section. At this point,
the x,y,z position you have calculated is still tentative. One ambiguity
remains; both x,y,z and -x,y,z can satisfy the difference vector equations
you have used so far. Both can account for the Harker peaks you observed
in the difference Patterson map. But, only one of these coordinates sets
is correct and will lead you to a beautiful electron density map, the other
is not correct and would lead to miserable phases and uninterpretable electron
density. There is a 50/50 chance that you got the sign of x correct.
The best way to determine whether x,y,z or -x,y,z is correct is to
calculate the u,v,w coordinates for a Patterson peak not lying on a Harker
section. Use one of the difference vector equations in the non-colored
box below. Check that this peak is present in the Patterson map (if the coordinates
of the peak fall outside the asymmetric unit, you can use a Patterson symmetry operator
to transform u, v, and w to values between 0.0 and 0.5). If you found
the peak, congratulations! If not, then simply change the sign of y
in your xyz coordinate describing the position of the heavy atom. Now
re-calculate u,v,w. You should be able to find the peak now.
7) Report one x,y,z position for the heavy atom site.
Make sure that you performed the check in step 6. Submit your x,y,z
coordinate to Mike or Duilio by the start of your next lab period. We will
check your answer during the lab.
summary slide
|
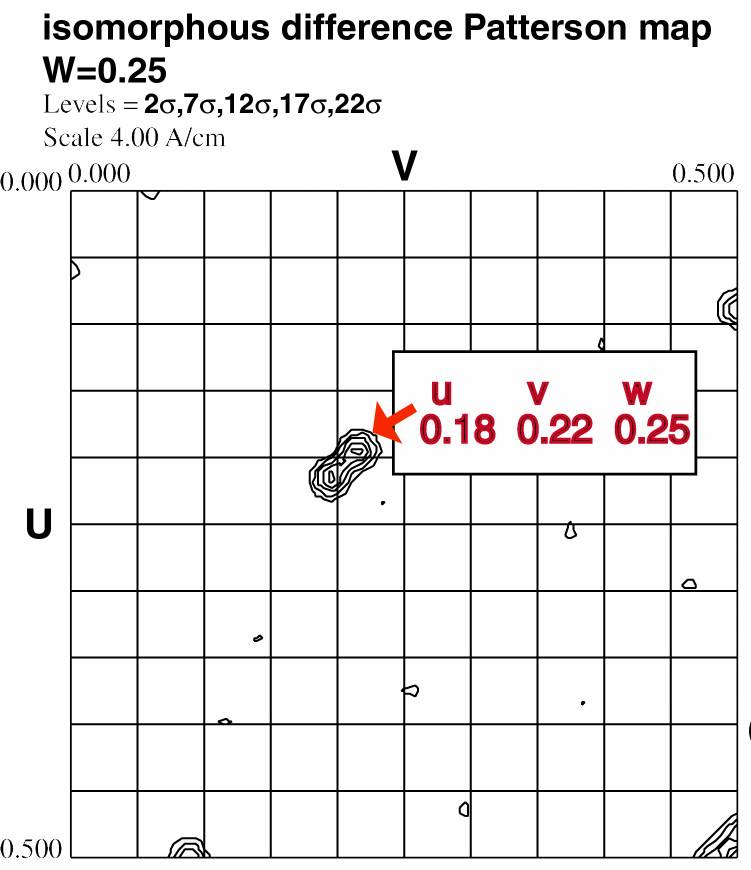
Step 1.
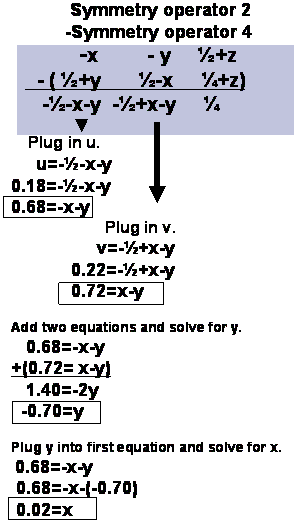
Steps 2 and 3.
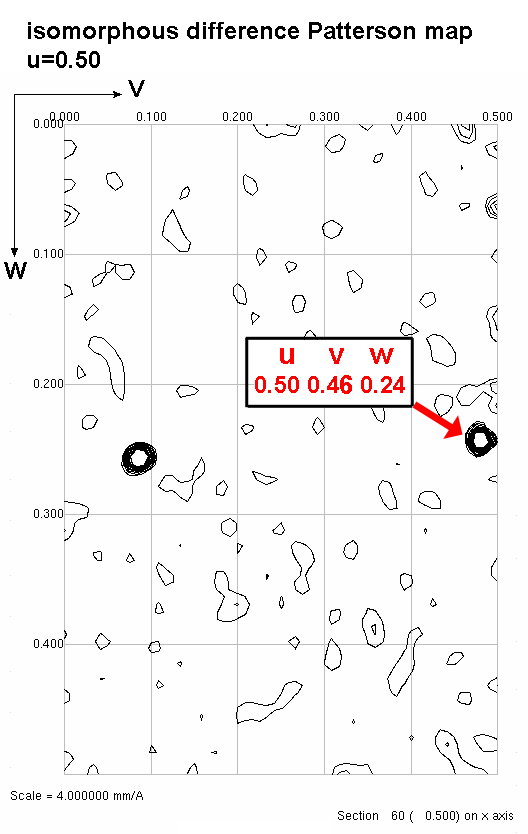
Step4a
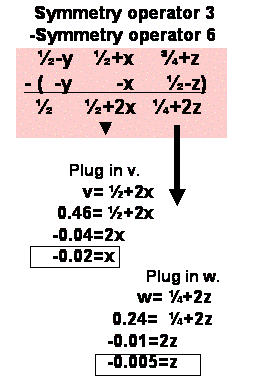
Step4

Step 5.
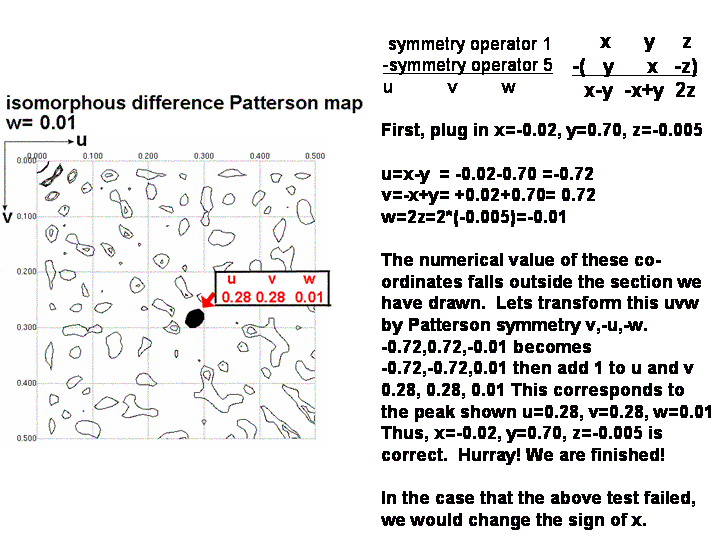
Step 6
|